Factor Models for High-dimensional Functional Time Series (part I & II)

Abstract

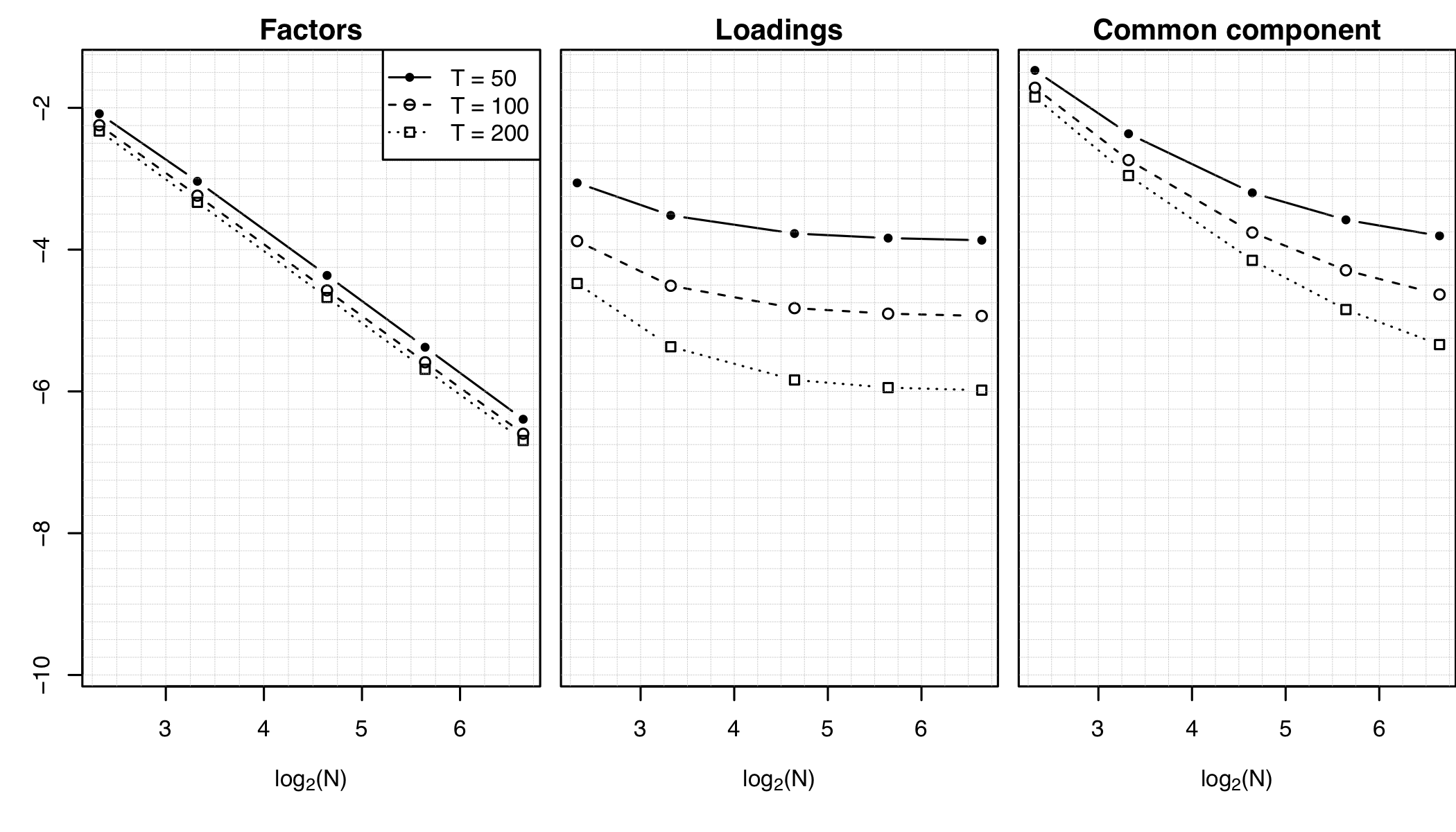
In this paper, we set up the theoretical foundations for a high-dimensional functional factor model approach in the analysis of large panels of functional time series (FTS). We first establish a representation result stating that if the first r eigenvalues of the covariance operator of a cross-section of N FTS are unbounded as N diverges and if the (r+1)th one is bounded, then we can represent each FTS as the sum of a common component driven by r factors, common to (almost) all the series, and a mildly cross-correlated idiosyncratic component (all the eigenvalues of the idiosyncratic covariance operator are bounded as N → ∞). Our model and theory are developed in a general Hilbert space setting that allows for panels mixing functional and scalar time series. We then turn to the identification of the number of factors, and the estimation of the factors, their loadings, and the common components. We provide a family of information criteria for identifying the number of factors, and prove their consistency. We provide average bounds for the estimators of the factors, loadings and common component; our results encompass the scalar case, for which they reproduce and extend, under weaker conditions, well-established similar results (Bai & Ng 2002). Under slightly stronger assumptions, we also provide uniform bounds, thus extending existing scalar results (Fan et al. 2013). Our consistency results in the asymptotic regime where the number N of series and the number T of time observations diverge thus extend to the functional context the “blessing of dimensionality” that explains the success of factor models in the analysis of high-dimensional (scalar) time series. We provide numerical illustrations and an application to forecasting mortality curves, where we demonstrate that our approach outperforms existing methods.