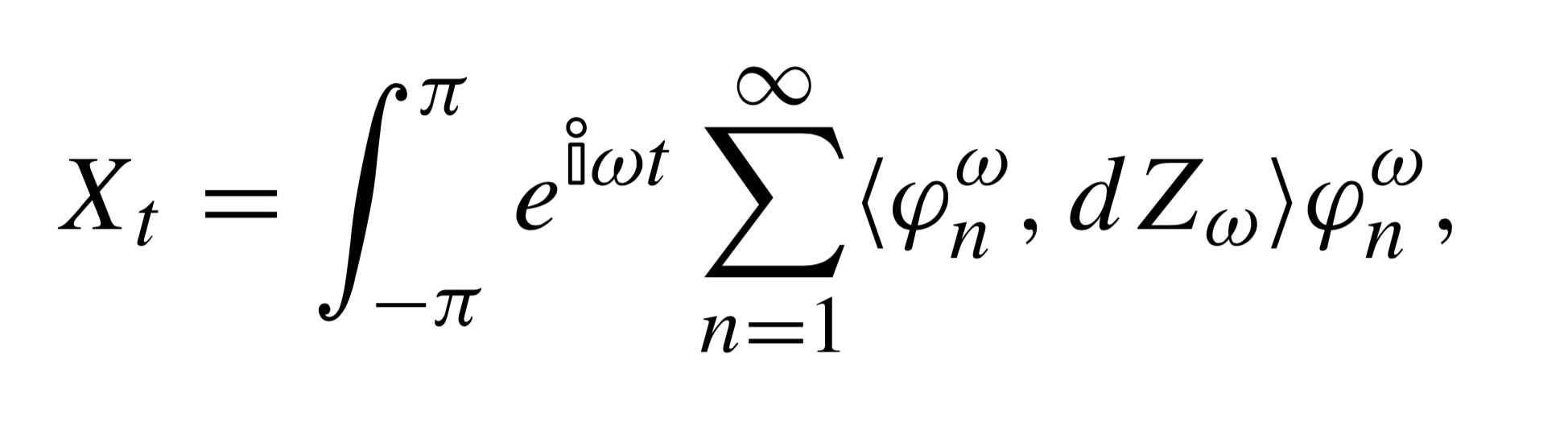
Cramér--Karhunen--Loève Representation and Harmonic Principal Component Analysis of Functional Time Series

Abstract

Results of this paper have been extended to the general setting of abstract separable Hilbert spaces, and presented in more depth in my PhD Thesis. We develop a doubly spectral representation of a stationary functional time series, and study the properties of its empirical version. The representation decomposes the time series into an integral of uncorrelated frequency components (Cramér representation), each of which is in turn expanded in a Karhunen–Loève series. The construction is based on the spectral density operator, the functional analogue of the spectral density matrix, whose eigenvalues and eigenfunctions at different frequencies provide the building blocks of the representation. By truncating the representation at a finite level, we obtain a harmonic principal component analysis of the time series, an optimal finite dimensional reduction of the time series that captures both the temporal dynamics of the process, as well as the within-curve dynamics. Empirical versions of the decompositions are introduced, and a rigorous analysis of their large-sample behaviour is provided, that does not require any prior structural assumptions such as linearity or Gaussianity of the functional time series, but rather hinges on Brillinger-type mixing conditions involving cumulants.